Clinical Trial Basics: Randomization in Clinical Trials

Introduction

Clinical trials represent a core pillar of advancing patient care and medical knowledge. Clinical trials are designed to thoroughly assess the effectiveness and safety of new drugs and treatments in the human population. There are 4 main phases of clinical trials, each with its own objectives and questions, and they can be designed in different ways depending on the study population, the treatment being tested, and the specific research hypotheses. The “gold standard” of clinical research are randomized controlled trials (RCTs), which aim to avoid bias by randomly assigning patients into different groups, which can then be compared to evaluate the new drug or treatment. The process of random assignment of patients to groups is called randomization.

Randomization in clinical trials is an essential concept for minimizing bias, ensuring fairness, and maximizing the statistical power of the study results. In this article, we will discuss the concept of randomization in clinical trials, why it is important, and go over some of the different randomization methods that are commonly used.

What does randomization mean in clinical trials?

Randomization in clinical trials involves assigning patients into two or more study groups according to a chosen randomization protocol (randomization method). Randomizing patients allows for directly comparing the outcomes between the different groups, thereby providing stronger evidence for any effects seen being a result of the treatment rather than due to chance or random variables.

What is the main purpose of randomization?

Randomization is considered a key element in clinical trials for ensuring unbiased treatment of patients and obtaining reliable, scientifically valuable results.[1] Randomization is important for generating comparable intervention groups and for ensuring that all patients have an equal chance of receiving the novel treatment under study. The systematic rule for the randomization process (known as “sequence generation”) reduces selection bias that could arise if researchers were to manually assign patients with better prognoses to specific study groups; steps must be taken to further ensure strict implementation of the sequence by preventing researchers and patients from knowing beforehand which group patients are destined for (known as “allocation sequence concealment”).[2]

Randomization also aims to remove the influence of external and prognostic variables to increase the statistical power of the results. Some researchers are opposed to randomization, instead supporting the use of statistical techniques such as analysis of covariance (ANCOVA) and multivariate ANCOVA to adjust for covariate imbalance after the study is completed, in the analysis stage. However, this post-adjustment approach might not be an ideal fit for every clinical trial because the researcher might be unaware of certain prognostic variables that could lead to unforeseen interaction effects and contaminate the data. Thus, the best way to avoid bias and the influence of external variables and thereby ensure the validity of statistical test results is to apply randomization in the clinical trial design stage.

Randomized controlled trials (RCTs): The ‘gold standard’

Randomized controlled trials, or RCTs, are considered the “gold standard” of clinical research because, by design, they feature minimized bias, high statistical power, and a strong ability to provide evidence that any clinical benefit observed results specifically from the study intervention (i.e., identifying cause-effect relationships between the intervention and the outcome).[3] A randomized controlled trial is one of the most effective studies for measuring the effectiveness of a new drug or intervention.

How are participants randomized? An introduction to randomization methods

Randomization includes a broad class of design techniques for clinical trials, and is not a single methodology. For randomization to be effective and reduce (rather than introduce) bias, a randomization schedule is required for assigning patients in an unbiased and systematic manner. Below is a brief overview of the main randomization techniques commonly used; further detail is given in the next sections.

Fixed vs. adaptive randomization

Randomization methods can be divided into fixed and adaptive randomization. Fixed randomization involves allocating patients to interventions using a fixed sequence that doesn’t change throughout the study. On the other hand, adaptive randomization involves assigning patients to groups in consideration of the characteristics of the patients already in the trial, and the randomization probabilities can change over the course of the study. Each of these techniques can be further subdivided:

Fixed allocation randomization methods:

Simple randomization: the simplest method of randomization, in which patient allocation is based on a single sequence of random assignments.
Block randomization: patients are first assigned to blocks of equal size, and then randomized within each block. This ensures balance in group sizes.

Stratified randomization: patients are first allocated to blocks (strata) designed to balance combinations of specific covariates (subject’s baseline characteristics), and then randomization is performed within each stratum.

Adaptive randomization methods:

Outcome-adaptive/results-adaptive randomization: involves allocating patients to study groups in consideration of other patients’ responses to the ongoing trial treatment. Minimization: involves minimizing imbalance amongst covariates by allocating new enrollments as a function of prior allocations

Below is a graphic summary of the breakdown we’ve just covered.

.rb-lazy { display: none; }

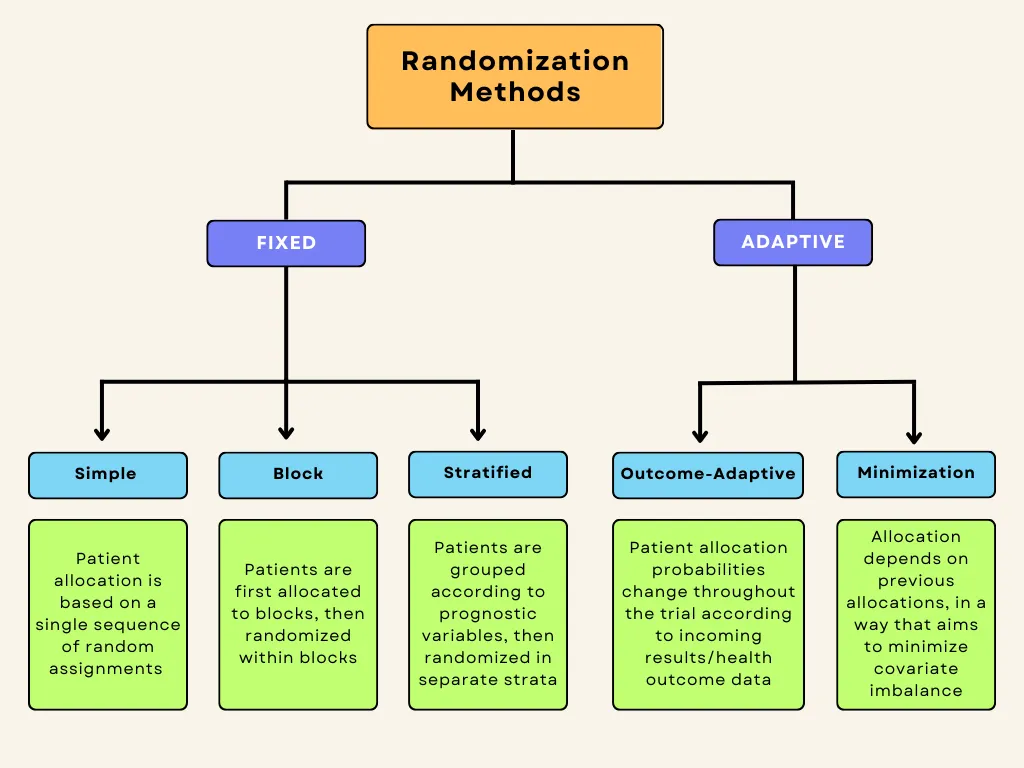
Fixed-allocation randomization in clinical trials

Here, we will discuss the three main fixed-allocation randomization types in more detail.

Simple Randomization

Simple randomization is the most commonly used method of fixed randomization, offering completely random patient allocation into the different study groups. It is based on a single sequence of random assignments and is not influenced by previous assignments. The benefits are that it is simple and it fulfills the allocation concealment requirement, ensuring that researchers, sponsors, and patients are unaware of which patient will be assigned to which treatment group. Simple randomization can be conceptualized, or even performed, by the following chance actions:

Flipping a coin (e.g., heads → control / tails → intervention)
Throwing a dice (e.g., 1-3 → control / 4-6 → intervention)
Using a deck of shuffled cards (e.g., red → control / black → intervention)
Using a computer-generated random number sequence
Using a random number table from a statistics textbook

There are certain disadvantages associated with simple randomization, namely that it does not take into consideration the influence of covariates, and it may lead to unequal sample sizes between groups. For clinical research studies with small sample sizes, the group sizes are more likely to be unequal.

Especially in smaller clinical trials, simple randomization can lead to covariate imbalance. It has been suggested that clinical trials enrolling at least 1,000 participants can essentially avoid random differences between treatment groups and minimize bias by using simple randomization.[4] On the other hand, the risks posed by imbalances in covariates and prognostic factors are more relevant in smaller clinical trials employing simple randomization, and thus, other methods such as blocking should be considered for such trials.

Block Randomization

Block randomization is a type of “constrained randomization” that is preferred for achieving balance in the sizes of treatment groups in smaller clinical trials. The first step is to select a block size. Blocks represent “subgroups” of participants who will be randomized in these subgroups, or blocks. Block size should be a multiple of the number of groups; for instance, if there are two groups, the block size can be 4, 6, 8, etc. Once block size is determined, then all possible different combinations (permutations) of assignment within the block are identified. Each block is then randomly assigned one of these permutations, and individuals in the block are allocated according to the specific pattern of the permuted block.[5]

Let’s consider a small clinical trial with two study groups (control and treatment) and 20 participants. In this situation, an allocation sequence based on blocked randomization would involve the following steps:

1. The researcher chooses block size: In this case, we will use a block size of 4 (which is a multiple of the number of study groups, 2).

2. All 6 possible balanced combinations of control (C) and treatment (T) allocations within each block are shown as follows:

TTCC
TCTC
TCCT
CTTC
CTCT
CCTT

3. These allocation sequences are randomly assigned to the blocks, which then determine the assignment of the 4 participants within each block. Let’s say the sequence TCCT is selected for block 1. The allocation would then be as follows:

Participant 1 → Treatment (T)
Participant 2 → Control (C)
Participant 3 → Control (C)
Participant 4 → Treatment (T)

We can see that blocked randomization ensures equal (or nearly equal, if for example enrollment is terminated early or the final target is not quite met) assignment to treatment groups.

There are disadvantages to blocked randomization. For one, if the investigators/researchers are not blinded (masked), then the condition of allocation concealment is not met, which could lead to selection bias. To illustrate this, let’s say that two of four participants have enrolled in block 2 of the above example, for which the randomly selected sequence is CCTT. In this case, the investigator would know that the next two participants for the current block would be assigned to the treatment group (T), which could influence his/her selection process. Keeping the investigator masked (blinded) or utilizing random block sizes are potential solutions for preventing this issue. Another drawback is that the determined blocks may still contain covariate imbalances. For instance, one block might have more participants with chronic or secondary illnesses.

Despite these drawbacks, block randomization is simple to implement and better than simple randomization for smaller clinical trials in that treatment groups will have an equal number of participants. Blinding researchers to block size or randomizing block size can reduce potential selection bias.[5]

Stratified Randomization

Stratified randomization aims to prevent imbalances amongst prognostic variables (or the patients’ baseline characteristics, also known as covariates) in the study groups. Stratified randomization is another type of constrained randomization, where participants are first grouped (“stratified”) into strata based on predetermined covariates, which could include such things as age, sex, comorbidities, etc. Block randomization is then applied within each of these strata separately, ensuring balance amongst prognostic variables as well as in group size.

The covariates of interest are determined by the researchers before enrollment begins, and are chosen based on the potential influence of each covariate on the dependent variable. Each covariate will have a given number of levels, and the product of the number of levels of all covariates determines the number of strata for the trial. For example, if two covariates are identified for a trial, each with two levels (let’s say age, divided into two levels [<50 and 50+], and height [<175 cm and 176+ cm]), a total of 4 strata will be created (2 x 2 = 4).

Patients are first assigned to the appropriate stratum according to these prognostic classifications, and then a randomization sequence is applied within each stratum. Block randomization is usually applied in order to guarantee balance between treatment groups in each stratum.

Stratified randomization can thus prevent covariate imbalance, which can be especially important in smaller clinical trials with few participants.[6] Nonetheless, stratification and imbalance control can become complex if too many covariates are considered, because an overly large number of strata can lead to imbalances in patient allocation due to small sample sizes within individual strata,. Thus, the number of strata should be kept to a minimum for the best results – in other words, only covariates with potentially important influences on study outcomes and results should be included.[6] Stratified randomization also reduces type I error, which describes “false positive” results, wherein differences in treatment outcomes are observed between groups despite the treatments being equal (for example, if the intervention group contained participants with overall better prognosis, it could be concluded that the intervention was effective, although in reality the effect was only due to their better initial prognosis and not the treatment).[5] Type II errors are also reduced, which describe “false negatives,” wherein actual differences in outcomes between groups are not noticed. The “power” of a trial to identify treatment effects is inversely related to these errors, which are related to variance between groups being compared; stratification reduces variance between groups and thus theoretically increases power. The required sample size decreases as power increases, which can also be used to explain why stratification is relatively more impactful with smaller sample sizes.

A major drawback of stratified randomization is that it requires identification of all participants before they can be allocated. Its utility is also disputed by some researchers, especially in the context of trials with large sample sizes, wherein covariates are more likely to be balanced naturally even when using simpler randomization techniques.[6]

Adaptive randomization in clinical trials

Adaptive randomization describes schemes in which treatment allocation probabilities are adjusted as the trial progresses.In adaptive randomization,allocation probabilities can be altered in order to either minimize imbalances in prognostic variables (covariate-adaptive randomization, or “minimization”), or to increase the allocation of patients to the treatment arm(s) showing better patient outcomes (“response-adaptive randomization”).[7] Adaptive randomization methods can thus address the issue of covariate imbalance, or can be employed to offer a unique ethical advantage in studies wherein preliminary or interim analyses indicate that one treatment arm is significantly more effective, maximizing potential therapeutic benefit for patients by increasing allocation to the most-effective treatment arm.

One of the main disadvantages associated with adaptive randomization methods is that they are time-consuming and complex; recalculation is necessary for each new patient or when any treatment arm is terminated.

Outcome-adaptive (response-adaptive) randomization

Outcome-adaptive randomization was first proposed in 1969 as “play-the-winner” treatment assignments.[8] This method involves adjusting the allocation probabilities based on the data and results being collected in the ongoing trial. The aim is to increase the ratio of patients being assigned to the more effective treatment arm, representing a significant ethical advantage especially for trials in which one or more treatments are clearly demonstrating promising therapeutic benefit. The maximization of therapeutic benefit for participants comes at the expense of statistical power, which is one of the major drawbacks of this randomization method.

Outcome-adaptive randomization can decrease power because, by increasing the allocation of participants to the more-effective treatment arm, which then in turn demonstrates better outcomes, an increasing bias toward that treatment arm is created. Thus, outcome-adaptive randomization is unsuitable for long-term phase III clinical trials requiring high statistical power, and some argue that the high design complexity is not warranted as the benefits offered are minimal (or can be achieved through other designs).[8]

Covariate-adaptive randomization (Minimization)

Minimization is a complex form of adaptive randomization which, similarly to stratified randomization, aims to maximize the balance amongst covariates between treatment groups. Rather than achieving this by initially stratifying participants into separate strata based on covariates and then randomizing, the first participants are allocated randomly and then each new allocation involves hypothetically allocating the new participant to all groups and calculating a resultant “imbalance score.” The participant will then be assigned in such a way that this covariate imbalance is minimized (hence the name minimization).[9]

A principal drawback of minimization is that it is labor-intensive due to frequent recalculation of imbalance scores as new patients enroll in the trial. However, there are web-based tools and computer programs that can be used to facilitate the recalculation and allocation processes.[10]

Conclusion

Randomization in clinical trials is important as it ensures fair allocation of patients to study groups and enables researchers to make accurate and valid comparisons. The choice of the specific randomization schedule will depend on the trial type/phase, sample size, research objectives, and the condition being treated. A balance should be sought between ease of implementation, prevention of bias, and maximization of power. To further minimize bias, considerations such as blinding and allocation concealment should be combined with randomization techniques.